LA VOCAZIONE STRINGATA DI UNA SUPERSIMMETRIA

 

 

Piergiorgio Odifreddi  lo conosco bene e da un pezzo, ebbene all'inizio del terzo millennio fece una intervista a Edward Witten il fisico di origine mediorientale ma di adozione statunitense, che è uno dei principali sostenitori della Teoria delle Super Stringhe  e la misteriosa M-Theory con quell'uso diffuso della parola Super che mi piace affibbiare anche a quella simmetria dell'inconscio postulata da Ignacio Mattè Blanco  nel suo "Inconscio come insiemi infiniti" : sono persuaso che un altro po' di "Super" per esempio quello da me individuato come 4^ figura della 2^ topica freudiana, ovvero dopo Al di là del principio del piacere, possa far pervenire a qualche cosa di nuovo in un ambito che vedrei di sinergia tra psicoanalisi e fisica quantistica:  intervista che vale la pena in parte di riportare nei suoi tratti piu' rilevanti. In principio c’erano 5 teorie delle stringhe. Cinque teorie delle stringhe tese a spiegare in maniera ancora incompleta la totalità delle regole che dirimono sulle dinamiche dell’universo, poi nel 1995 in un convegno di fisici quantistici Witten si  concentrò proprio su quste teorie e decise di….eliminarne qualcuna.Fu così che, in una atmostera galvanizzata – come fa notare Brian Greene in numerosi documentari dedicati a Witten - questi  stupì i fisici teorici colà convenuti proponendo alla loro attenzione una diversa, quanto spettacolare, prospettiva di osservazione delle teorie delle stringhe già cogitate. Tempo dopo, ricordando quella conferenza,  Leonard Susskind un altro grande padre della teoria delle stringhe,  rivelò che quando Witten iniziò a parlare, non ebbe piu' dubbi ne' perplessita'  nell'accettare  la cosiddetta M-Teoria o M-Theory, che in sostanza con l'unificazione di tutte le teorie note delle stringhe, diventava proprio questa M-Theory  

Una M-theory che non ha mai saputo chiarire il ruolo della M nel nome (alcuni speculano che tale consonante sia in realtà la W di Witten rovesciata, altri ritengono che voglia dire mistero, magia, matrix, madre, mostro, finanche madness, ovvero follia!). Cos’è dunque la M-Theory? La M-Theory è semplicemente una diversa prospettiva di approccio alla teoria delle stringhe. Nello specifico matematico (della matematica formidabile utilizzata!), le equazioni di Witten hanno dimostrato che le cinque teorie delle stringhe esistenti erano in realtà solo cinque modi differenti di guardare alla stessa… faccenda. Insomma, per certi versi Witten ha validato i lavori dei teorici che lo avevano preceduto e ha dato nuova dignità e nuova energia alla speculazione fisica di cui si erano sempre occupati. Naturalmente la M-Theory portava seco anche delle conseguenze “tecniche” importanti e ben precise che giustificavano il cambiamento della prospettiva di visione proposto. Fino a quel momento, infatti, la multidimensionalità supportata dalle diverse teorie delle stringhe indicava in numero di 10 le dimensioni fisiche esistenti: una temporale, tre spaziali e 6 dimensioni extra piuttosto piccole e invisibili ai nostri sensi. La M-Theory, invece, per poter “funzionare” al meglio necessitava di utilizzare 11 dimensioni: il genio di Witten ha quindi messo in campo una nuova dimensione extra mai considerata prima. Va notato difatti che  la teoria delle stringhe era gia' dal 1968 quando le sue prime risoluzioni furono scoperte dal fisico italiano Gabriele Veneziano  la piu' accreditata candidata a proporsi  come espressione di una Teoria del Tutto, ovvero l'idea unificante  della teoria della relativita' e della meccanica quantistica, che fece sognare Einstein e che ha anche rappresentato il sogno di tutta una vita dello sfortunato Stephen Hawking  Con Witten  la teoria delle stringhe è diventata uno spettacolo di fuochi d'artificio intellettuali che ha illuminato diverse zone d'ombra della matematica e della fisica, e che un giorno forse farà luce sul mistero stesso dell'universo. Per godere di qualche scintilla di questo spettacolo pirotecnico, ecco dunque che Oddifreddi ando' a trovare Witten e gli fece tale intervista 

Di recente una sua intervista è apparsa sull'Espresso, col titolo "Dio gioca a dadi", e il giorno dopo l'Avvenire ha commentato: "Vedete? Il nuovo Newton crede in Dio". Cominciamo dunque a chiarire questo punto: c'è qualche connessione tra scienza e religione? 

Sono cose molto diverse. E per la comprensione dell'universo, la scienza è più efficace della religione. 

E lei è credente?

 Le scoperte scientifiche non incoraggiano la fede religiosa.

 C'è invece una connessione tra la teoria delle stringhe e il pitagorismo?

 Non conosco abbastanza il pitagorismo per poter rispondere, ma credo che nessuna delle filosofie antiche influenzi il pensiero degli scienziati moderni. 

Nemmeno l'armonia delle sfere, cioè la relazione fra matematica, fisica e musica? 

 In senso letterale, la cosa è falsa: in fondo, la musica è costituita da onde che si propagano nell'aria. 

E in senso metaforico?

 C'è effettivamente un'analogia interessante. La ricchezza dei suoni prodotti dalle corde di un violino o di un piano deriva dal fatto che ciascuna di esse vibra in tanti modi, chiamati armoniche. Un do, ad esempio, suona molto diverso sul piano o su un diapason, che invece produce un suono puro. Se si suonassero dei pezzi soltanto con dei diapason, l'effetto sarebbe molto brutto. 

Helmoltz ha provato a dirigere un'orchestra di diapason, nell'Ottocento. 

Sarà stato terribile. Ora, anche le stringhe che io studio possono vibrare in tanti modi, e ciascuno di essi viene interpretato come una particella elementare. Questa è la chiave per unificare le varie particelle: come diverse forme di vibrazione di un'unica stringa.

 Lei parla di stringhe, ma non ci sono anche membrane? Cioè, non solo strumenti a corda, ma anche a percussione? 

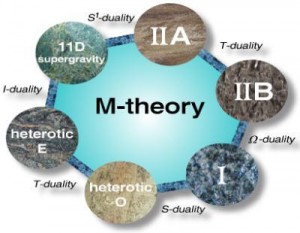
La teoria moderna, che si chiama M-teoria, è una reinterpretazione della teoria delle stringhe. 

A proposito, che cosa significa "M"?

 Matrice, ma anche Magia o Mistero. Perché la sua natura non è ancora completamente compresa, certamente molto meno della teoria delle stringhe, che ne costituisce il limite quando gli effetti quantistici sono piccoli. 

L'arte della magia e del mistero non stanno proprio nel fatto che la natura è matematica? 

Certamente il mondo fisico è descritto da strutture e teorie matematiche eleganti e di grande bellezza, che hanno una loro logica interna precisa ed esigente: non sappiamo perché, ma è così. E col passare del tempo le teorie diventano sempre più stringenti e ricche. 

Qualcuno si lamenta però che i suoi sono ragionamenti da fisico, e non vere dimostrazioni da matematico.

 In parte hanno ragione. Il fatto è che molte idee interessanti in geometria sono venute dalla teoria quantistica dei campi, la più importante teoria fisica del Novecento, che non è affatto ben compresa matematicamente: quelle idee quindi non sono ancora state sistematizzate. Ci sono due vie complementari da seguire, per farlo: sviluppare la matematica necessaria, e comprendere meglio la fisica coinvolta. Fino ad allora, benché la cosa sia frustrante, bisognerà accontentarsi di idee stimolanti senza dimostrazioni rigorose. 

Altri invece si lamentano che la sua è matematica pura, di interesse più metafisico che fisico. 

La teoria delle stringhe ha già giocato un ruolo importante nella fisica contemporanea, ad esempio permettendo interessanti e sorprendenti intuizioni sul problema del confinamento dei quark: il fatto, cioè, che non li si possa mai osservare isolati. Inoltre ha prodotto l'idea della supersimmetria, alcuni effetti della quale sono già stati verificati da vent'anni, anche se non si sono ancora trovate le superparticelle predette dalla teoria. In questo forse i critici esagerano un po’. 

Che cosa corrisponde, nella teoria delle stringhe, alle equazioni di campo di Einstein nella relatività generale, o alle equazioni d'onda di Schrodinger e Dirac nella meccanica quantistica? 

Le equazioni principali non si conoscono ancora, e questo è appunto il maggior problema aperto. Il motivo è che, invece di partire da certe idee ben definite e costruirci sopra una teoria, come fece Einstein con la relatività generale, ci siamo trovati fra le mani una teoria senza capire bene su che idee sia basata. 

E dalle equazioni della teoria si potranno ricavare, come casi speciali, quelle di Einstein, Schrodinger e Dirac? 

Chi lo sa? Bisognerebbe sapere quanto sono difficili da risolvere, una volta trovate. Ma certamente questa è una delle cose che mi incuriosiscono di più, perché ci direbbe che cosa è veramente la teoria e ci darebbe l'ispirazione per nuove idee, sia in matematica che in fisica. 

Benché lei voli alto in matematica, non sembra il tipico matematico che vive nelle nuvole. In particolare, lavora per la pace in Medioriente. 

Sì, questo è un problema che mi sta a cuore. Ho vissuto in Israele per un anno, quando ne avevo dodici, e da venti lavoro con un gruppo chiamato "Shalom Achshav". a differenza della matematica, purtroppo, la politica non si basa sulla ragione.